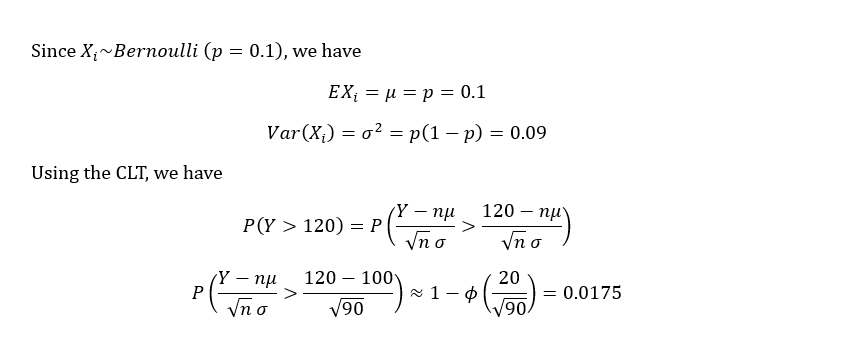Central Limit Theorem
The central limit theorem (CLT) states that, under certain conditions, the sum of a large number of random variables is approximately normal. It explains how the sampling distribution of the mean behaves as the sample size increases.
When we repeatedly take random samples of size n from a population with:
- A mean μ, and a finite variance σ2
The sampling distribution of the sample mean will:
- Approach a normal distribution as n→∞.
- Have the same mean μ as the population mean.
- Have a variance σ2.
Assumptions of the CLT
- Independence:
The assumption of independence requires that the samples or observations are independent of each other. This means that the value of one observation should not influence or depend on the value of another. Independence is crucial because it ensures that each observation provides unique information about the population, and the combined data accurately represent the overall population characteristics.
For instance, consider a study measuring the heights of students in a school. If we select one student and then choose their sibling as the next sample, the measurements may not be independent, as siblings often have similar genetic and environmental influences on height. To maintain independence, random sampling methods, such as simple random sampling, are typically employed. Violations of this assumption can lead to biased results and misinterpretations of the CLT’s applicability.
- Sample Size:
The size of the sample plays a crucial role in the CLT. While the theorem holds true for any sample size in cases where the population is already normally distributed, for non-normally distributed populations, a sufficiently large sample size is required for the sampling distribution to approximate normality. In most practical scenarios, a sample size of n≥30 is considered adequate for the CLT to apply, although this threshold can vary depending on the population’s underlying distribution.
For example, if the population distribution is heavily skewed or contains outliers, larger samples may be necessary for the sample mean’s distribution to resemble a normal curve. Conversely, for populations that are nearly symmetric or uniform, smaller sample sizes may suffice. This assumption highlights the importance of collecting enough data to ensure the reliability of statistical inferences based on the CLT.
- Finite Variance:
Another critical assumption is that the population variance (σ2) must be finite. This condition ensures that the variability within the population is bounded, making it possible to calculate meaningful sample means. Infinite or undefined variance can occur in theoretical distributions, such as the Cauchy distribution, where the CLT does not apply because the sample mean fails to converge.
For example, in a population of test scores, if the variance is finite, it implies that most scores cluster around the mean, with fewer extreme deviations. This finiteness of variance stabilizes the sampling process, allowing the mean of the sample to reliably represent the population mean as the sample size grows. When the population variance is infinite or unknown, alternative statistical methods may be required, as the assumptions underlying the CLT are violated.
Why the CLT is Important?
- Foundation for Normal Approximation:
- Even if the population is not normally distributed (e.g., it’s skewed or uniform), the sample mean will tend to follow a normal distribution for large n.
- Enables Statistical Inference:
- Since the sample mean is approximately normal, we can use normal distribution properties (e.g., z-scores, confidence intervals) to make predictions about the population. Specific distribution will not be needed.
Example:
In a communication system each data packet consists of 1000 bits. Due to the noise, each bit may be received in error with probability 0.1. It is assumed bit errors occurs independently. Find the probability that there are more than 120 errors in a certain data packet.
Solution.
Let us define as the indicator random variable for the bit in the packet. That is, if the bit is received in error, and otherwise. Then the are and If is the total number of bit errors in the packet, we have