Measures of Dispersion
There are two main types of dispersion methods in statistics which are:
- Absolute Measure of Dispersion:
An absolute measure of dispersion contains the same unit as the original data set. Absolute dispersion method expresses the variations in terms of the average of deviations of observations like standard or mean deviations.
The types of absolute measures of dispersion are:
- Range: It is simply the difference between the maximum value and the minimum value given in a data set. Example: 1, 3,5, 6, 7 => Range = 7 -1= 6
- Standard Deviation: It measures the absolute dispersion or variability of a distribution. It is denoted as .
When deviations are taken from actual mean:


- Variance: Deduct the mean from each data in the set then squaring each of them and adding each square and finally dividing them by the total no of values in the data set is the variance. Variance is also denoted as square of standard deviation (2)
- Quartiles and Quartile Deviation: The quartiles are values that divide a list of numbers into quarters. The quartile deviation is half of the distance between the third and the first quartile.
(Q3 – Q1) / 2
- Mean and Mean Deviation: The average of numbers is known as the mean and the arithmetic mean of the absolute deviations of the observations from a measure of central tendency is known as the mean deviation.
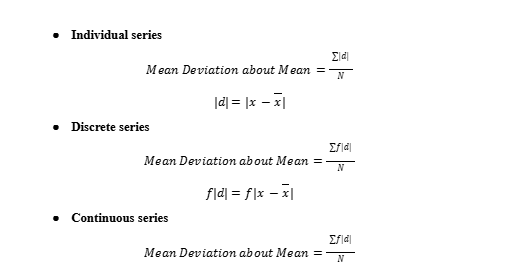
2. Relative Measure of Dispersion:
The relative measures of dispersion are used to compare the distribution of two or more data sets. This measure compares values without units. Common relative

