Probability Distributions
A probability distribution describes how the values of a random variable are distributed. It provides the probabilities of occurrence of different possible outcomes in an experiment.
Probability distribution is mainly of two types:
- Discrete Probability Distributions: We say that a random variable X has a discrete distribution or that X is a discrete random variable if X can take only a finite number k of different values or, at most, an infinite sequence of different values
Examples of discrete probability distribution:
- Uniform Distribution
- Bernoulli Distribution
- Binomial Distribution
- Negative Binomial Distribution
- Geometric Distribution
- Poisson Distribution
- Continuous Probability Distributions: We say that a random variable X has a continuous distribution or that X is a continuous random variable if there exists a nonnegative function , defined on the real line, such that for every interval of real numbers (bounded or unbounded), the probability that X takes a value in the interval is the integral of over the interval.

Examples of continuous probability distribution:
- Uniform Distribution
- Chi-square Distribution
- Log-Normal Distribution
- Student T Distribution
- Standard Normal Distribution
- Exponential Distribution
Discrete Probability Distributions
- Bernoulli Distribution
The Bernoulli distribution models a random variable that can take only two possible outcomes, labelled as “success” and “failure” or 1 and 0.
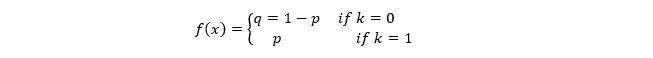
2. Binomial Distribution
The binomial distribution has a sequence of multiple independent Bernoulli trials. Each Bernoulli trial is independent and has only two possible outcomes, typically labeled as success (S) and failure (F). The probability of success, denoted as p, remains the same for each trial. There are fixed number of trials.
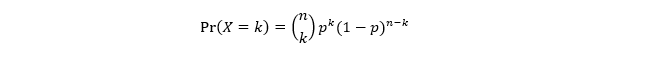
3. Negative Binomial Distribution
The negative binomial distribution talks about the distribution of the number of (failed and successful) trials needed to get the defined number of successes.
4. Geometric Distribution
Geometric distribution calculates the number of failures before the first success occurs.
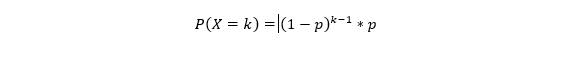
5. Poisson Distribution
The Poisson distribution models the number of rare events that occur in a fixed time or space interval. The Poisson distribution is characterized by lambda, λ, the mean number of occurrences in the interval.
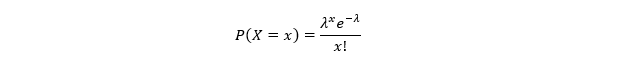
Continuous Probability Distribution
1.Chi-Square Distribution
Chi-square distribution is used to determine whether the differences between observed and expected data are significant. In simpler terms, it is like a threshold that helps in determining if the relationship between categorical variables in a study is real or if it could likely occur randomly. It is defined as the distribution of the sum of the squares of k independent standard normal random variables.
2.Log Normal Distribution
The Log-Normal distribution is a continuous probability distribution of a random variable whose logarithm follows a normal distribution. If Y=ln(X) is normally distributed, then X follows a log-normal distribution.
3.Standard Normal Distribution
Standard normal distribution, also known as the z-distribution, is a special type of normal distribution. In this distribution, the mean (average) is 0 and the standard deviation (a measure of spread) is 1.
Each normal CDF is converted to the standard normal CDF as follows:
4. Student T Distribution
Student’s t-distribution is a probability distribution that is used for making inferences about the population mean when the sample size is small or when the population standard deviation is unknown.
The formula for calculating the T-score in the context of a t-distribution is given by:
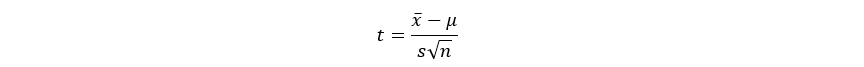
5. Exponential Distribution
The exponential distribution is a continuous probability distribution used to model the time elapsed before a given event occurs.
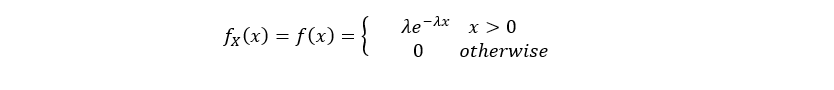
The parameter is called rate parameter.
